斜率优化DP | Yuhang's Blog

考虑如下形式的状态转移方程： $$ f(i) = \max_{j < i} \{ y(j) - x(j) k(i) \} +h(i) $$ 其中$x(j),y(j),k(i),h(i)$皆为已知函数。去掉$\max$函数，可变形为： $$ y(j) = k(i)x(j) + h(i)-f(i) $$ 可以看作是：对于所有小于$i$的$j$，$(x(j), y(j))$确定了平面上的一系列点。斜率为定值$k(i)$的直线经过其中的一个点，当该直线的纵截距为最小时，$f(i)$取到最大值。不难发现所有符合条件的点必然在一个凸包上。例如，当$k(i) > 0$时，欲使得纵截距最小，则所有的点必然在一个下凸包上，而最优决策点需要使得它与它之后的点连线的斜率恰好大于$k(i)$。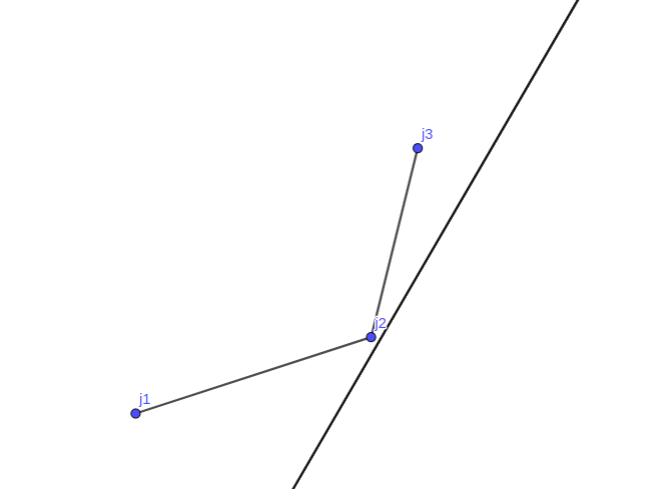一条我们需要找的直线

当$x(j)$单调不减的时候，每次都在凸包的最右侧插入点，因此可以用一个单调队列维护，保证入队前清除队尾凸包内的点即可。
- 若同时$k(i)$也单调不减，则由图形易知最优决策点也满足单调不减，因此可以不断弹出不符合条件的队首，则剩下的第一个点就是最优决策点。
- 若$k(i)$不具有单调性，则需要维护整个凸包，并二分查找最优决策点。
当$x(j)$不具有单调性，要么采用splay来对凸包进行动态插入，要么使用CDQ分治处理。此处略去。CDQ分治可参考这里。

注意事项：

和高中数学一样，注意讨论斜率不存在的情形，将不存在的斜率视$y$的差值的正负设为正无穷或负无穷；
队列初始有一个$0$，并始终保证队列中至少有一个元素；
理解清除队尾点的时候slope(q[r-1], q[r])>=slope(q[r-1], i)的几何意义。

例题

洛谷P3195

#include <bits/stdc++.h>
using namespace std;
#define rep(i,from,to) for(register int i=(int)(from);i<=(int)(to);++i)
#define For(i,to) for(register int i=0;i<(int)(to);++i)
typedef long long ll;
inline ll read(){
    ll x=0; ll sign=1; char c=getchar();
    while(c>'9'  c<'0') {if (c=='-') sign=-1;c=getchar();}
    while(c>='0' && c<='9'){x=(x<<3)+(x<<1)+c-'0';c=getchar();}
    return x*sign;
}
#define N 51234
int n; ll L; ll c[N];
ll s[N], a[N], b[N];
ll q[N]; int l, r;
ll f[N];

#define square(x) ((x)*(x))
#define yy(j) (f[j]+b[j]*b[j])
#define xx(j) (b[j])
// I didn't consider cases where slope doesn't exist, which could
// potentially cause errors
#define slope(j1,j2) (double)(yy(j2)-yy(j1))/(xx(j2)-xx(j1))
int main() {
    n = read(), L = read();
    b[0]=1+L;
    rep(i,1,n) {
        c[i]=read();
        s[i]=s[i-1]+c[i];
        a[i]=s[i]+i;
        b[i]=s[i]+1+L+i;
    }

    l = 1, r = 1;
    q[1] = 0;
    rep(i,1,n) {
        while(l<r && slope(q[l], q[l+1]) < (double)2*a[i]) l++;
        f[i] = f[q[l]]+square(a[i] - b[q[l]]);
        while(l<r && slope(q[r-1], i) < slope(q[r-1], q[r])) r--;
        q[++r] = i;
    }
    cout << f[n] << endl;
    return 0;
}

洛谷P5875

#include <bits/stdc++.h>
using namespace std;
#define rep(i,from,to) for(register int i=(int)(from);i<=(int)(to);++i)
#define rev(i,from,to) for(register int i=(int)(from);i>=(int)(to);--i)
#define For(i,to) for(register int i=0;i<(int)(to);++i)
typedef long long ll;
inline ll read(){
    ll x=0; ll sign=1; char c=getchar();
    while(c>'9'  c<'0') {if (c=='-') sign=-1;c=getchar();}
    while(c>='0' && c<='9'){x=(x<<3)+(x<<1)+c-'0';c=getchar();}
    return x*sign;
}
#define N 312345
ll n, st[N], sc[N], q[N], l, r, s, f[N];

ll xx(ll j) {return sc[j];}
ll yy(ll j) {return f[j]-s*sc[j];}
ll dx(ll j1, ll j2) {return xx(j1)-xx(j2);}
ll dy(ll j1, ll j2) {return yy(j1)-yy(j2);}
double slope(ll j1, ll j2) {
    if (dx(j1, j2) == 0) return dy(j1, j2) > 0 ? 1.0/0.0 : -1.0/0.0;
    else return (double)dy(j1, j2) / dx(j1, j2);
}

ll binary_search(ll k) {
    if (l==r) return q[l];
    ll L = l; ll R = r;
    while (L < R) {
        ll M = (L + R) >> 1;
        if (slope(q[M+1], q[M]) <= (double)k) L = M + 1;
        else R = M;
    }
    return q[L];
}

int main() {
    n=read(),s=read();
    rep(i,1,n){
        st[i]=st[i-1]+read();
        sc[i]=sc[i-1]+read();
    }
    l=r=1;
    rep(i,1,n){
        ll j = binary_search(st[i]);
        f[i] = f[j]+st[i]*(sc[i]-sc[j])+s*(sc[n]-sc[j]);
        while(l<r && slope(q[r-1], q[r])>=slope(q[r-1], i)) --r;
        q[++r] = i;
    }
    cout<<f[n]<<"\n";

    return 0;
}